La Ecuación Cuadrática: Un Viaje Milenario del Pensamiento Humano

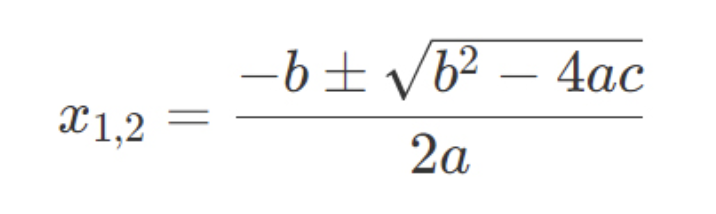
Desentrañando el Origen de una Fórmula Clave

¿Alguna vez te has preguntado de dónde viene esa famosa fórmula que resuelve las ecuaciones de segundo grado, la que empieza con "menos b más menos la raíz..."? No es el invento de un único genio moderno, sino el resultado de un viaje fascinante que abarca miles de años y diversas civilizaciones. Es como una historia detectivesca de la inteligencia humana, donde cada cultura, a su manera, dejó una pista crucial para resolver uno de los enigmas matemáticos más fundamentales. Prepárate para viajar en el tiempo y descubrir cómo esta ecuación, que hoy resuelves en tu secundaria o bachillerato, fue en su momento un desafío que impulsó el desarrollo del pensamiento abstracto.

Los Primeros Acertijos: De Mesopotamia a las Pirámides

Cuando los Babilonios Sumaban Tierras (c. 2000-1800 a.C.)

Imagina la antigua Mesopotamia, con sus vastos campos de trigo y complejos sistemas de canales de riego. Hace unos 4000 años, los babilonios ya se enfrentaban a problemas prácticos que hoy resolveríamos con una ecuación de segundo grado. No tenían nuestra notación, ni mucho menos la fórmula. ¡Ni siquiera usaban un álgebra como la nuestra! Su enfoque era más geométrico y numérico.

Por ejemplo, querían calcular las dimensiones de un terreno si conocían su área y una relación entre sus lados. Para esto, desarrollaron un método ingenioso que hoy llamamos "completar el cuadrado". Piensa en ello como si tuvieran un cuadrado incompleto de tierra y supieran cómo añadirle un pedazo para que fuera un cuadrado perfecto, y así calcular su lado. No buscaban una fórmula universal, sino métodos precisos para casos específicos. Su matemática era pragmática, nacida de la necesidad de administrar imperios y recursos.

Egipto: Más Rudimentario, Pero Presente (c. 1850 a.C.)

Un poco más tarde, en el místico Egipto, los escribas y constructores también se toparon con problemas que implicaban ecuaciones cuadráticas, principalmente al calcular áreas o volúmenes para sus imponentes construcciones. Sus métodos, vistos en papiros como el de Moscú o el de Rhind, eran más específicos para cada caso y no tan sofisticados como los babilónicos. No había una fórmula explícita, sino aproximaciones ingeniosas. La matemática egipcia, aunque no tan abstracta, demostraba que el desafío de las relaciones cuadráticas surgía naturalmente en distintas civilizaciones.

La Fórmula Toma Forma: Asia y el Mundo Árabe

La India Antigua: ¡Nace la Semilla de la Fórmula! (c. 800 a.C. - 668 d.C.)

Mucho antes de que Europa occidental se interesara seriamente en estos problemas, la India antigua ya estaba haciendo avances asombrosos. En las escuelas de los Sulba Sutras, se resolvían problemas cuadráticos ligados a la construcción de altares. Pero el verdadero "salto" lo dio Brahmagupta (siglo VII d.C.). En su tratado Brahmasphutasiddhanta, este genio indio no solo formuló una solución general para las ecuaciones cuadráticas (¡sí, una versión temprana de la famosa fórmula!), sino que además ¡trabajó con números negativos! En una era donde incluso en otras culturas los números negativos eran vistos con recelo, Brahmagupta ya lidiaba con ellos y con las raíces imaginarias. Fue una ruptura paradigmática, un paso crucial hacia el álgebra abstracta.

Grecia Clásica: La Belleza de la Geometría (c. 500-300 a.C.)

Los griegos, obsesionados con la geometría y la demostración lógica, abordaron las ecuaciones cuadráticas de una forma muy visual. Figuras como Euclides, en sus Elementos, resolvían problemas equivalentes a estas ecuaciones, pero usando construcciones geométricas. Era como si dijeran: "No calcularemos el número, ¡lo dibujaremos y demostraremos su existencia en el espacio!" No buscaron una fórmula algebraica general, pero su rigor geométrico y su énfasis en la prueba sentaron bases importantes para futuros desarrollos matemáticos.

El Mundo Islámico: El Álgebra Cobra Nombre (c. 800-1200 d.C.)

Aquí es donde la historia da un giro decisivo. El matemático persa Al-Juarismi (siglo IX d.C.) fue el gran sistematizador. Su nombre dio origen a la palabra "álgebra" (¡sí, de su libro Al-Jabr!). Al-Juarismi no solo clasificó las ecuaciones cuadráticas en seis tipos, sino que proporcionó métodos tanto geométricos como puramente algebraicos para resolverlas, basándose en la idea de "completar el cuadrado". Su obra fue el puente de oro que transmitió todo el conocimiento babilónico e indio, a través del árabe, hacia Europa. Su enfoque algebraico y general marcó un hito ineludible.

El Camino Hacia la Ecuación Moderna y sus Aplicaciones Ubicuas

Europa Medieval y Renacimiento: El Despertar del Álgebra (c. 1200-1600 d.C.)

Con la llegada de los textos árabes traducidos, el conocimiento de la ecuación cuadrática floreció en Europa. Leonardo de Pisa (Fibonacci), en su Liber Abaci, introdujo estos métodos. Más tarde, en el Renacimiento, matemáticos italianos como Girolamo Cardano (famoso por las cúbicas) refinaron el entendimiento de las cuadráticas, incluyendo el uso de raíces negativas y complejas, sentando las bases para el álgebra moderna.

La Edad Moderna: La Fórmula Universal (siglos XVII-XIX)

Finalmente, en la Edad Moderna, la ecuación cuadrática adopta su forma familiar. François Viète (siglo XVI) fue un visionario al introducir el uso de letras (como a,b,c) para representar coeficientes, lo que permitió expresar la ecuación de forma general y elegante. Ya no eran solo problemas específicos, sino una estructura abstracta. Más tarde, René Descartes y Pierre de Fermat conectaron las ecuaciones cuadráticas con las parábolas en la geometría analítica, dándoles un significado visual que aún hoy usamos para entenderlas.

La famosa fórmula cuadrática, se estandarizó en esta época. Es el resultado de miles de años de mentes brillantes, desde Babilonia hasta Europa, pasando por India y el mundo islámico.

El Problema de las Luces: Optimizando la Iluminación con Matemáticas

Imagina que estás en un pasillo o en un espacio donde necesitas iluminar un punto específico en el suelo, por ejemplo, el centro de un escenario pequeño, una mesa de exhibición o un lugar donde quieres que la luz sea máxima. Tienes dos focos de luz, y sabes a qué altura están colgados (desde el techo), pero necesitas saber a qué distancia horizontal desde ese punto central debes colocarlos para que la iluminación sea la mejor posible.

Aquí es donde entra el "problema de las luces". Aunque pueda parecer algo de física avanzada, el corazón de su solución está en una ecuación de segundo grado.

La lógica es esta:

1. Intensidad de la Luz: La intensidad de la luz que llega a una superficie no solo depende de la potencia del foco, sino también de la distancia a la que se encuentra y del ángulo con el que incide.

   • Distancia: Cuanto más lejos está una luz, menos intensa es (disminuye con el cuadrado de la distancia).

   • Ángulo: La luz es más efectiva cuando incide perpendicularmente. Si incide muy inclinada, se "dispersa" más.

2. El Dilema: Tienes dos focos colgados a una altura fija sobre el punto central que quieres iluminar. Si los pones directamente encima (distancia horizontal cero), la luz incide bien, pero puede ser demasiado directa y solo un foco "casi" ilumina el centro. Si los alejas demasiado, la luz se vuelve muy débil. Queremos encontrar el "punto dulce" donde ambos focos contribuyan a la máxima iluminación conjunta en ese punto específico.

¿Cómo se traduce a una ecuación de segundo grado?

Aunque la fórmula final puede parecer compleja a primera vista (porque involucra la ley del inverso del cuadrado y el coseno del ángulo de incidencia), al simplificarla para optimizar la posición (es decir, encontrar la distancia horizontal 'x' óptima), la relación matemática que surge es una ecuación cuadrática.

Por ejemplo, si tienes dos focos de igual potencia colgados a una altura 'h' y quieres maximizar la iluminación en el punto central del suelo, la intensidad total de la luz en ese punto (I) se puede expresar como una función de la distancia horizontal 'x' a la que colocas los focos desde el centro. Para encontrar el valor de 'x' que maximiza 'I', se utiliza el cálculo (derivadas), pero los puntos críticos (donde la iluminación es máxima o mínima) se encuentran al resolver una ecuación que, tras las simplificaciones, se convierte en una de segundo grado.

En esencia, la ecuación de segundo grado nos ayuda a encontrar esa distancia horizontal 'x' óptima que equilibra la distancia (para que la luz no se debilite demasiado) y el ángulo de incidencia (para que la luz sea efectiva) de ambos focos, logrando así la mejor iluminación conjunta en el punto deseado.

Así que, la próxima vez que veas dos luces inteligentemente colocadas para iluminar algo, puedes recordar que detrás de esa aparente simplicidad, hubo una ecuación de segundo grado ayudando a encontrar el lugar exacto donde debían estar. Es un ejemplo concreto de cómo las matemáticas son una herramienta poderosa para optimizar y resolver problemas prácticos en el diseño y la ingeniería.

La Ecuación Cuadrática: Un Testamento al Progreso

En síntesis, la ecuación de segundo grado no es solo una fórmula en tu libro de texto; es un testamento a la perseverancia humana y a la colaboración intercultural. Su desarrollo nos muestra que el conocimiento se construye paso a paso, con la contribución de mentes brillantes a lo largo de milenios. Es un recordatorio de que, incluso en los problemas más "simples" de hoy, reside una historia épica de descubrimiento y asombro, una historia que nos invita a seguir explorando los misterios del universo con la misma curiosidad.